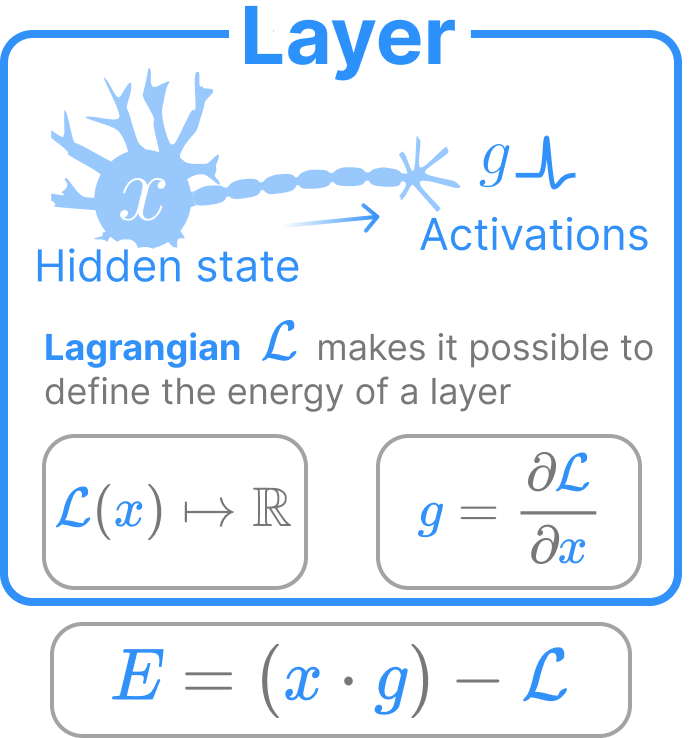
Neuron Layers

Turning Lagrangians into building blocks for our network
Hopfield Layer Description
The energy fundamentals of a Neuron Layer.

Fundamentally, a neuron layer is nothing more than a lagrangian function on top of data. This Lagrangian completely defines both an energy and an activation for the layer. In practice, we additionally specify the following in addition to the Lagrangian:

Our neuron layers are extensions of the neuron layer as it is commonly incorporated in feedforward architectures. The primary difference is that our neuron layers evolve their state \(x\) over time and have a bounded energy function on their states. The energy function of our neuron is completely defined by its Lagrangian \(\mathcal{L}\)

\[E_\text{layer} = \sum\limits_i x_i g_i - \mathcal{L}(x)\]

where \(g = \nabla_x \mathcal{L}\) are the “activations”. The first component is a summation of the elementwise multiplication between \(x\) and \(g\). The second term is the Lagrangian. This energy function is the direct consequence of the Legendre transform on the Lagrangian.

We can view a neuron layer of shape (D,) as a collection of \(D\) neurons holding scalar data. Convolutional networks frequently have activations defined atop images or image patches of shape (H,W,D). We can view layers of this shape as a collection of \(D\) neurons each of shape \((H,W)\). Lagrangians that reduce over a particular dimension (e.g., the softmax) will typically reduce over the neuron dimension \(D\).

source

Layer

 Layer (lagrangian:treex.module.Module, shape:Tuple[int], tau:float=1.0,
        use_bias:bool=False, init_lagrangian=False, name:str=None,
        **kwargs)

The energy building block of any activation in our network that we want to hold state over time

Type Default Details
lagrangian Module Factory function creating lagrangian module describing
shape typing.Tuple[int] Number and shape of neuron assembly
tau float 1.0 Time constant
use_bias bool False Add bias?
init_lagrangian bool False Initialize the lagrangian with kwargs?
name str None Overwrite default class name, if provided
kwargs

Initialize with a lagrangian

Layer(LExp(beta=5.), (32,32,3))
Layer {
    bias: None,
    lagrangian: LExp {
        beta: 5.0,          Parameter
        min_beta: 1e-06,
        name: "lexp",       str
    },
    name: "layer",          str
    shape: tuple [
        32,
        32,
        3,
    ],
    tau: 1.0,
    use_bias: False,
}

source

Layer.energy

 Layer.energy (x)

The predefined energy of a layer, defined for any lagrangian

source

Layer.__call__

 Layer.__call__ (x)

Alias for self.energy. Helps simplify treex’s .init method

source

Layer.activation

 Layer.activation (x)

The derivative of the lagrangian is our activation or Gain function g.

Defined to operate over input states x of shape self.shape

source

Layer.g

 Layer.g (x)

Alias for self.activation

source

Layer.init_state

 Layer.init_state (bs:int=None, rng=None)

Initialize the states of this layer, with correct shape.

If bs is provided, return tensor of shape (bs, *self.shape), otherwise return self.shape By default, initialize layer state to all 0.

Type Default Details
bs int None Batch size
rng NoneType None If given, initialize states from a normal distribution with this key

Convenience Layers

It is nice to package commonly used lagrangians into their own kind of layers, e.g., IdentityLayers or SoftmaxLayers. We create a helper function to do that in this section.

source

MakeLayer

 MakeLayer (lagrangian_factory:Callable, name:Optional[str]=None)

Hack to make it easy to create new layers from Layer utility class.

delegates modifies the signature for all Layers. We want a different signature for each type of layer.

So we redefine a local version of layer and delegate that for type inference.

Type Default Details
lagrangian_factory typing.Callable
name typing.Optional[str] None Name of the new class

Our utility that we use to create these “convenience layers” is a bit hacky, but it works by injecting the lagrangian and the expected arguments for the lagrangian into our Layer utility. However, the hack loses the ability to inspect docstrings of the original neuron layer.

Energy Analysis

Most of all, every neuron layer has an energy. This is defined by the following equation:

\[E_\text{layer} = \sum\limits_i x_i g_i - \mathcal{L}(x)\]

The first component is a summation of the elementwise multiplication between \(x\) and \(g\). The second term is the lagrangian.

Let us create a layer with state \(x\) and initial state \(x_0\). Let us then evolve \(x\) over time by simply descending the energy of the neuron layer. Note that this neuron layer is not connected to anything, but we still expect it to reach a fixed point where the energy of the layer reaches a fixed point.

\[\tau\frac{dx}{dt} = -\frac{dE_\text{layer}}{dx}\]

Code 
shape = (5,); key = jax.random.PRNGKey(0); k1, k2, key = jax.random.split(key,3)
layer = ExpLayer(shape,beta=1.).init(k1, jnp.ones(shape))
x0 = layer.init_state(rng=k2)

@ft.partial(jax.jit, static_argnames=("alpha",))
def next_x(layer:Layer, # Neuron layer
           x:jnp.ndarray, # Current state
           alpha:float): # Step size
    dEdx = jax.value_and_grad(layer.energy)
    E, dx = dEdx(x)
    next_x = x -alpha * dx
    return E, next_x

x = x0
Es = []
for i in range(100):
    E, x = next_x(layer, x, 0.1)
    Es.append(E)
    
fig, ax = plt.subplots(1)
ax.plot(np.stack(Es))
ax.set_title("Energy of a disconnected neuron layer over time")
ax.set_ylabel("Energy")
ax.set_xlabel("Timesteps")
plt.show(fig)
2022-12-02 01:13:11.068186: E external/org_tensorflow/tensorflow/compiler/xla/stream_executor/cuda/cuda_driver.cc:267] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)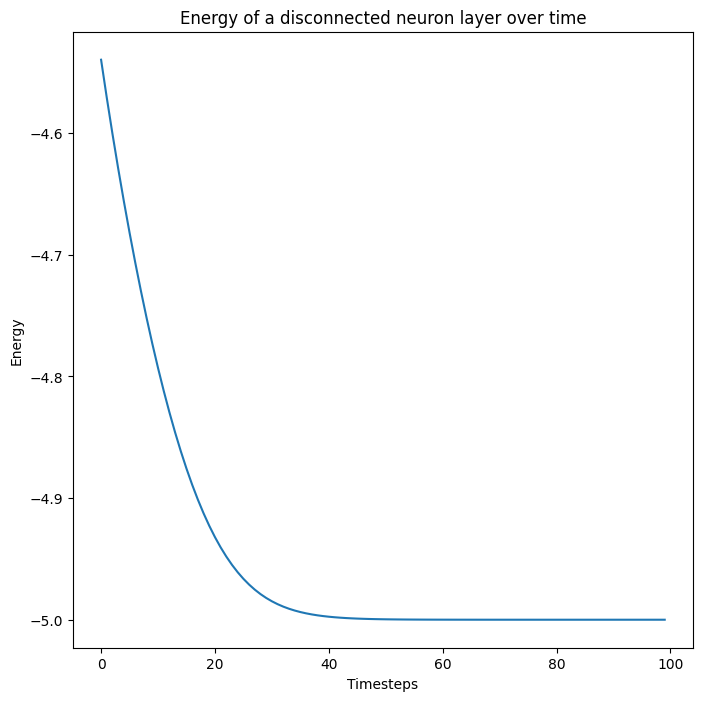

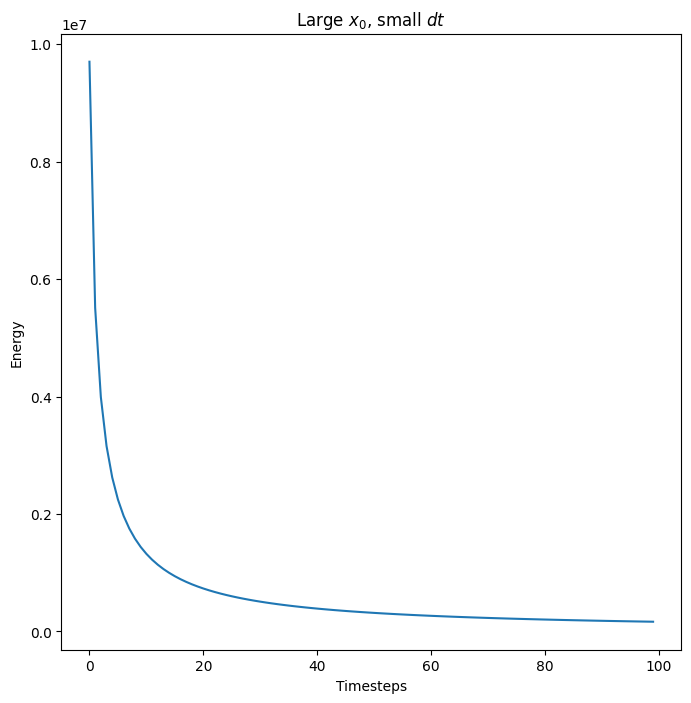
The energy is bounded for any initial neuron state \(x\) (though at some point the values are numerically too large for the exponential we are using as the activation function)

Code 
x = 100*x0
Es = []
for i in range(100):
    E, x = next_x(layer, x, 5e-8)
    Es.append(E)
    
fig, ax = plt.subplots(1)
ax.plot(np.stack(Es))
ax.set_title("Large $x_0$, small $dt$")
ax.set_ylabel("Energy")
ax.set_xlabel("Timesteps")
plt.show(fig)